2024. 1. 10. 18:00ㆍ@dev.formegusto

우리의 일상은 알게 모르게 많은 것들이 분류되어 조화를 이루고 있습니다. 근데 어딘가 익숙하면서 어색한 단어로 느껴지네요. 그래서 이번 기회에 스스로 분류라는 단어에 대해서 생각해 보았는데요. 무언가를 카테고리별로 정리하는 것을 뜻하기도 하지만 이들의 특성을 분석하고 도출하여 규칙 그리고 결정 등을 내리는 데에 활용까지 할 수 있는 행위인 것 같네요.
📚 Learning Point
- KMeans Overview
- KMeans Process
- KMeans++
- KMeans and KMeans++ Difference
머신러닝 분야에서 이러한 현실 세계의 특징이 적용된 군집화, Clustering이라고 불리우는 개념이 존재하는데요. 그중에서도 가장 유명하고 해당 스터디의 최종 목표로 하고 있는 KMeans Clustering의 기초적인 개념을 알아보도록 하겠습니다. 이번 챕터에서는 원활한 설명을 위하여 파이썬을 사용하도록 할게요. 😉😉
🫧 KMeans Overview
군집화(Clustering)는 데이터 집합 내 데이터에 유사성(Similarity)을 측정하는 계산식을 기반으로 여러 개의 군집(Cluster)으로 분류하는 비지도 학습(Unsupervised Learning)의 패러다임 중 하나입니다.
| Cluster 0 | Cluster 1 | Cluster 2 | Cluster 3 |
| 강아지 | 고래 | 진달래 | 치킨 |
| 고양이 | 상어 | 민들래 | 피자 |
해당 알고리즘이 진행된 데이터 집합의 데이터들은 각자 속한 군집의 번호를 부여받게 되는데요. 이는 범주형 데이터의 특징을 가지고 있기 때문에 다양한 분야에서 분석의 용도로 사용하거나 인공지능 모델에 사용할 정답값(Label) 및 추가적인 특징(Feature)을 만들기 위한 활용으로 이어집니다.
from sklearn.cluster import KMeans그중에서도 KMeans Clustering은 간단한 프로세스 대비 높은 성능을 보여주기 때문에 많은 사랑을 받고 있어요. 그 때문에 교육에서도 군집화를 설명하는 데에 자주 언급되는 알고리즘인데요. 이를 가장 빠르게 만나보는 방법은 파이썬의 머신러닝 라이브러리인 사이킷런(scikit-learn)을 통해서입니다.
K = 3
kmeans = KMeans(n_clusters=K)해당 라이브러리의 KMeans를 객체를 만들 때에 전달하는 대표적인 매개변수 중에 n_clusters가 있는데요. 이는 KMeans의 하이퍼 파라미터인 K라는 변수를 나타냅니다. 이는 데이터 집합에서 몇 개의 군집을 형성하도록 할 것인지에 대한 내용을 포함합니다.
| length | width |
| 1.4 | 0.2 |
| 4.6 | 1.3 |
| ... | |
kmeans.fit(data)KMeans 모델을 학습시키는 데에 가장 이상적인 입력 데이터는 2개의 특징값을 가지는 데이터입니다. x와 y값을 표현할 수 있는 포인트 형태의 데이터로 볼 수 있어요. 해당 데이터를 생성한 모델 객체의 fit 메서드로 입력해주면 학습이 진행됩니다.
📚 Main Variables
- kmeans.labels_ - 군집 번호 부여 정보 ex) [1, 1, .. 2, 2]
- kmeans.cluster_centers_ - 군집의 중심점 값 ex) [[4.27, 1.34], [1.46, 0.246], [5.6, 2.03]]
- kmeans.inertia_ - 군집 별 오차제곱합(SSE, Sum of Squared Error)의 합계 ex) 31.37
학습이 완료된 KMeans 모델은 3개의 주요 변수를 확인해 주면 되는데요.

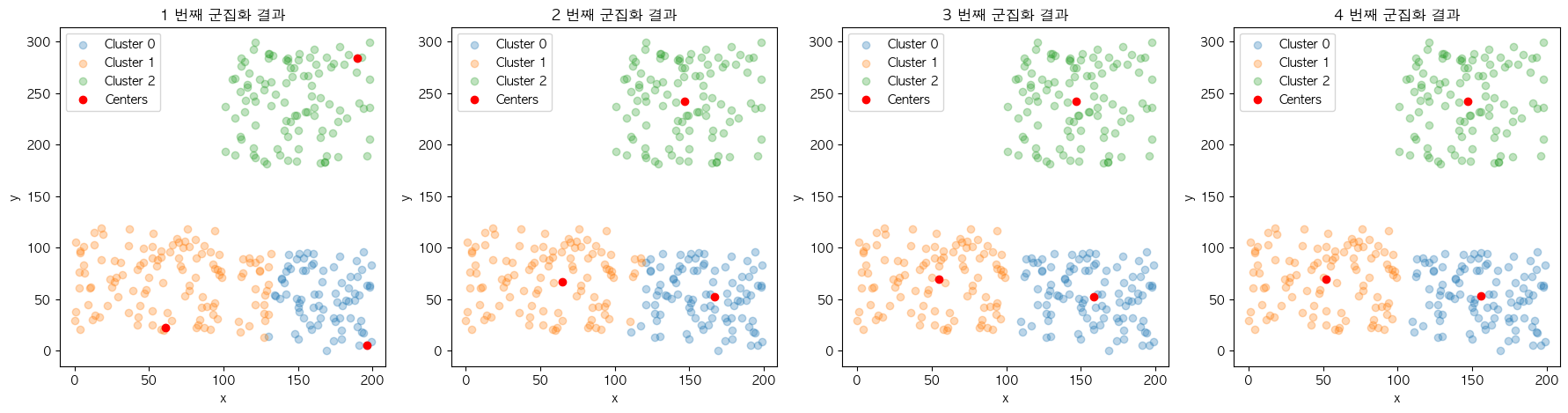
이 중에서 labels_ 변수를 기존 데이터 집합에 반영하여 색깔별로 각 데이터가 부여받은 군집번호를 표현하였고 cluster_centers_ 변수를 추가적으로 표시하여 군집화 결과를 시각화할 수 있습니다. 여기서 우리는 K개로 설정한 중심점을 기준으로 거리가 가까운 데이터 포인트 간에 군집을 이루었다는 것을 확인할 수가 있죠. 👏🏻👏🏻

그리고 이를 실제 분류와 육안만으로 비교해 보았을 때 거의 유사하게 분류되었다는 것을 알 수 있는데요. 이와 같이 실세계의 무언가를 나타내는 데이터는 같은 계열끼리 대부분 비슷한 특징을 가진다는 점에 기초하여 분류를 진행하는 것이 KMeans 알고리즘의 접근법 입니다.
✨ KMeans Process
KMeans는 매개변수인 K를 중심점의 개수로 사용하며 이를 기준으로 적절한 군집을 찾아가는 프로세스로 구성되어 있습니다.
🐶 KMeans Steps
- K개의 초기 중심점 설정
- 중심점과 데이터 간의 거리 계산
- 최소 거리 중심점의 군집 번호를 데이터에 부여
- 군집 별 평균값을 계산하여 중심점에 반영
- 2~4의 과정을 중심점에 변화가 없을 때까지 반복
적절한 군집을 찾기 위하여 초기에 설정된 중심점과 데이터 집합 간의 거리 계산과 구성된 군집의 평균값을 중심점에 반영하는 과정을 반복적으로 진행하는데요.
import numpy as np
K = 3
centers_idx = np.random.choice(range(len(dataset)), size=K)
cluster_centers = dataset[centers_idx]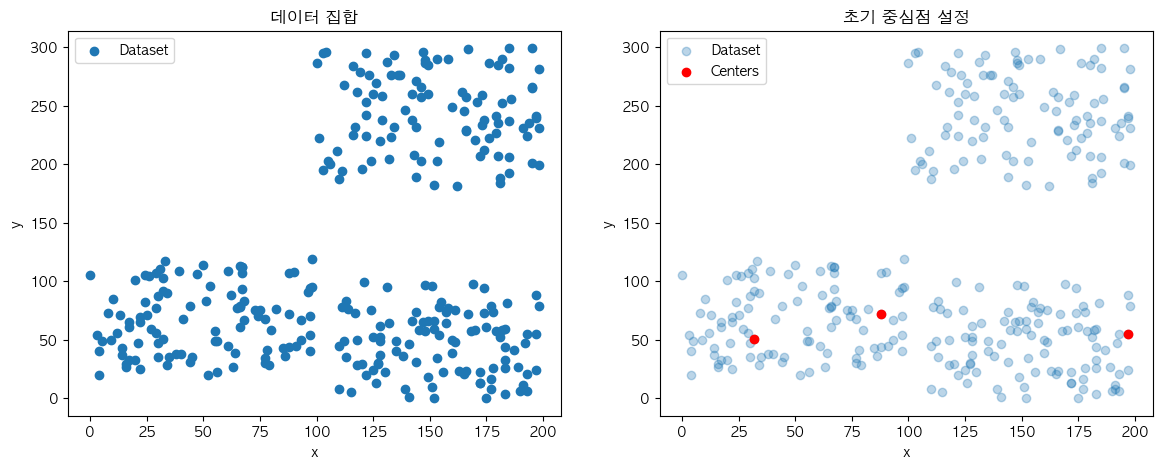
K개의 초기 중심점을 설정하는 방법으로는 가장 일반적인 데이터 집합 내에서 K개의 데이터를 무작위로 선택하는 방법이 있습니다.
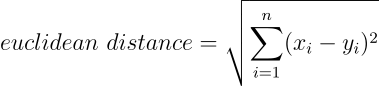
중심점과 데이터 간의 거리 계산에는 대표적인 유사도 함수 중 하나인 유클리디안 거리(Euclidean Distance)를 사용합니다.
from sklearn.metrics.pairwise import euclidean_distances
distances = euclidean_distances(dataset, cluster_centers)| centroids[0] | centroids[1] | centroids[2] | |
| dataset[0] | 170.99 | 210.66 | 195.23 |
| dataset[1] | 110.57 | 158.82 | 29.12 |
| dataset[2] | 184.17 | 221.14 | 211.73 |
| ... | |||
이는 여러 개의 특징을 동일한 수량으로 가지는 두 데이터 간의 유사성을 특징 간의 오차제곱합의 제곱근을 기반으로 측정하며 값이 높을수록 유사성이 떨어지는 데이터로 구별합니다. 데이터 포인트의 형태인 해당 문제에서는 거리가 멀리 떨어져 있다로도 해석할 수 있습니다.
labels = distances.argmin(axis=1)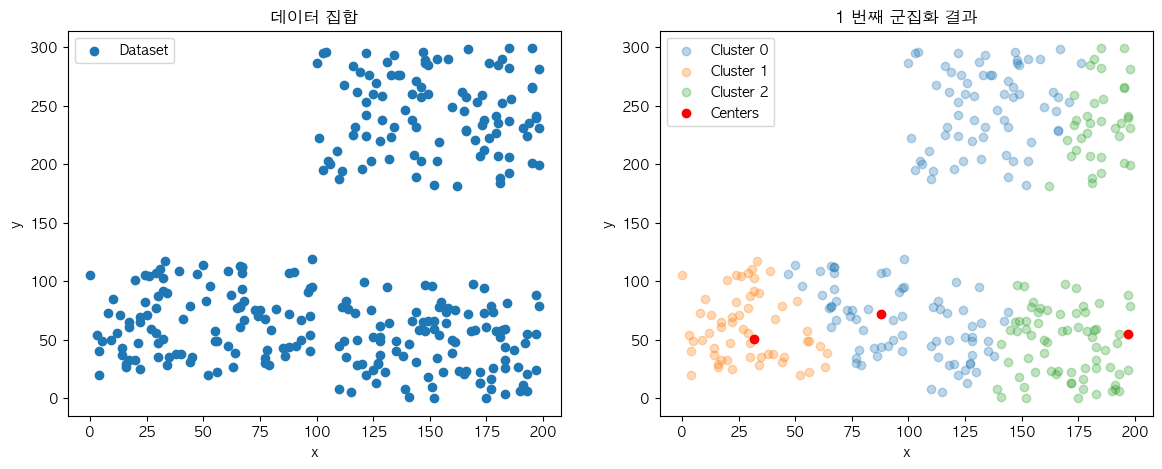
최소 거리 중심점의 군집 번호를 데이터에 부여하는 단계에서 이러한 유사도 측정 결과를 사용하는데요. 데이터 별로 가장 측정값이 가장 낮은 중심점의 인덱스 값을 군집 번호로 부여받게 됩니다. 데이터 입장에서는 자신과 가장 가까운 중심점에 종속되는 것이죠.
next_centers = cluster_centers.copy()
for cluster_no in range(len(cluster_centers)):
members = dataset[labels == cluster_no]
next_centers[cluster_no] = members.mean(axis=0)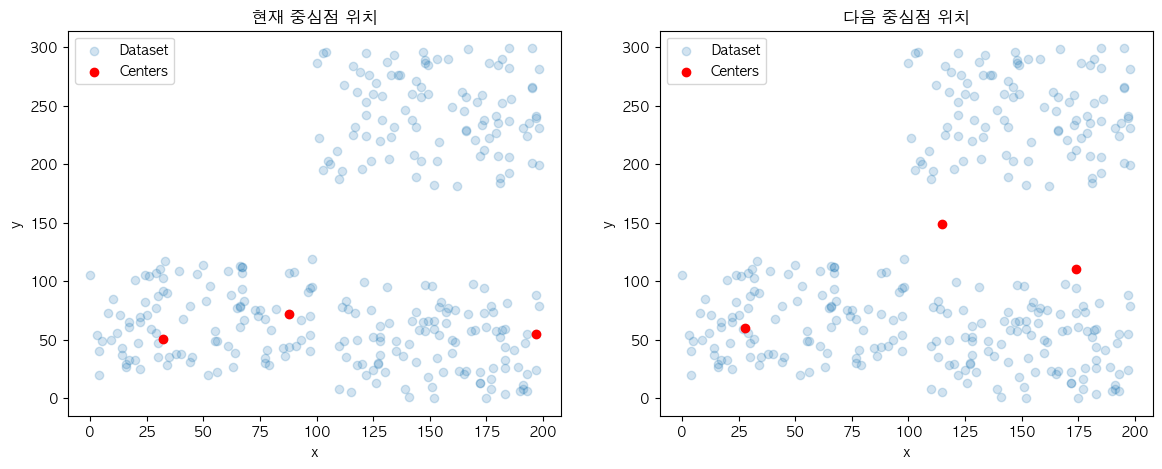
군집 별 평균값을 계산하여 중심점에 반영하는 과정은 중심점을 이동시킨다라고도 표현하는데요.
while True:
# 2. 중심점과 데이터 간의 거리 계산
distances = euclidean_distances(dataset, cluster_centers)
# 3. 최소 거리 중심점의 군집 번호를 데이터에게 부여
labels = distances.argmin(axis=1)
# 4. 군집 별 평균값을 계산하여 중심점에 반영
next_centers = cluster_centers.copy()
for cluster_no in range(len(cluster_centers)):
members = dataset[labels == cluster_no]
next_centers[cluster_no] = members.mean(axis=0)
# 5. 2~4의 과정을 중심점에 변화가 없을 때 까지 반복
is_equal = np.all(cluster_centers == next_centers)
if is_equal:
break
else:
cluster_centers = next_centers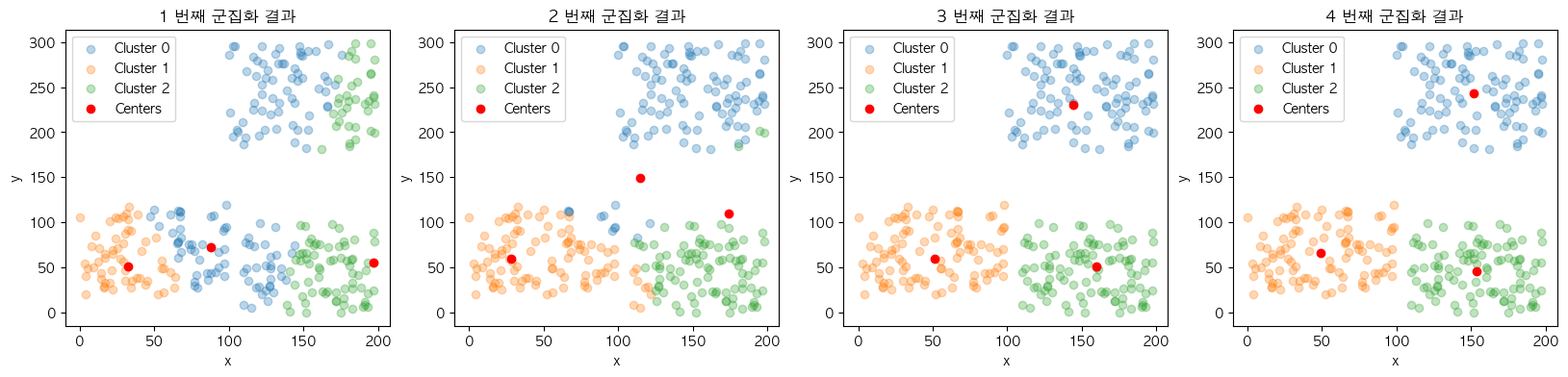
2~4의 과정을 중심점에 변화가 없을 때까지 반복 단계의 근거가 됩니다. 중심점을 이동시켰기 때문에 거리계산부터 다시 프로세스를 진행하게 되었을 때 다른 군집 구조를 만들어낼 가능성이 있는데요. 반대로 중심점에 변화가 없을 경우에는 이전 군집 구조와 변화한 게 없다는 것으로 추측할 수 있기 때문에 이를 종료 조건으로 사용합니다.
| cluster_centers | labels | inertia | |
| 1 | [ 88, 72], [ 32, 51], [197, 55] | [0, 2, 0, ... , 2, 0, 1] | 3,767,833 |
| 2 | [115, 149], [ 28, 60], [174, 110] | [0, 2, 0, ... , 2, 1, 1] | 1,989,651 |
| 3 | [144, 230], [ 51, 59], [160, 51] | [0, 2, 0, ... , 2, 1, 1] | 535,653 |
| 4 | [152, 243], [ 49, 66], [154, 46] | [0, 2, 0, ... , 2, 1, 1] | 499,057 |
진행될수록 각 군집의 중심점과 해당 군집에 속한 데이터 간의 오차제곱합(SSE; Sum of Squares Error)의 총합인 inertia 값이 점차 작아지는데요. 이는 각 군집의 응집도가 높아지도록 유도하는 KMeans 프로세스의 특징을 확인시켜 줍니다.
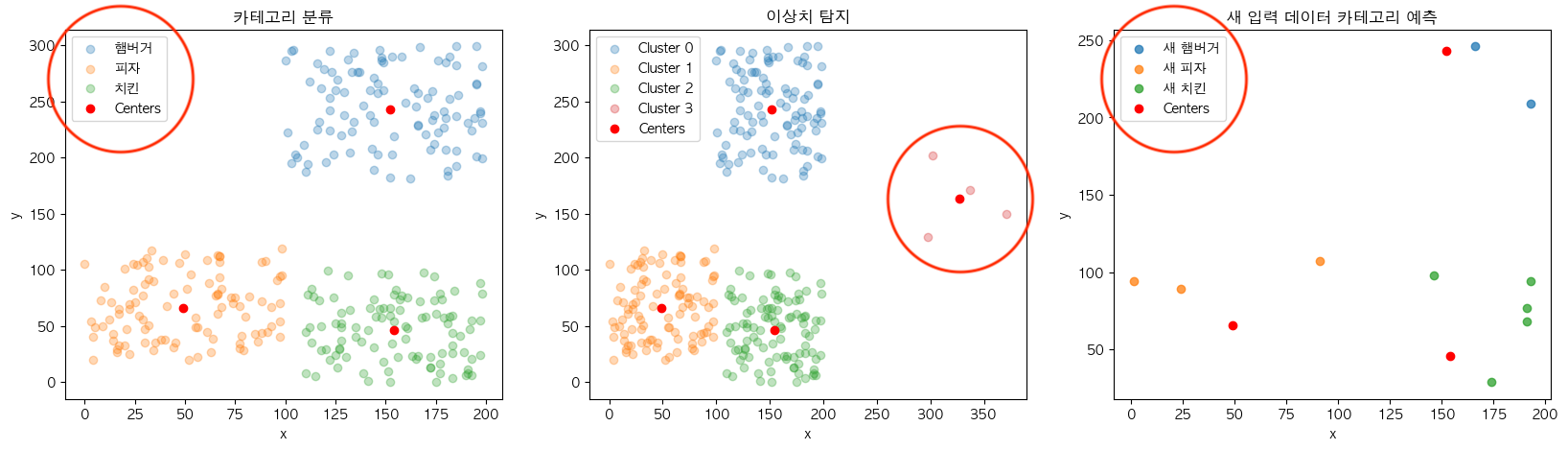
학습이 완료된 KMeans 모델은 변수들은 대표적으로 분류를 통한 데이터 분석, 이상치 탐지 그리고 예측 등에 사용될 수 있는데요. 이 외에도 마치 우리가 규칙 및 결정 등과 같은 여러 목적에 맞게 분류를 사용하는 것과 같이 폭넓게 활용할 수 있습니다.
❄️ KMeans++
일반 KMeans는 대표적으로 2가지의 발생가능한 문제점을 가지고 있습니다.
📍 Possible Normal KMeans Problems.
- 학습 시간 지연
- 결과의 불규칙성
이는 KMeans의 프로세스 중에서 K개의 초기 중심점을 설정하는 단계에서 무작위로 선택하는 방식 때문에 발생하는 상황들인데요.
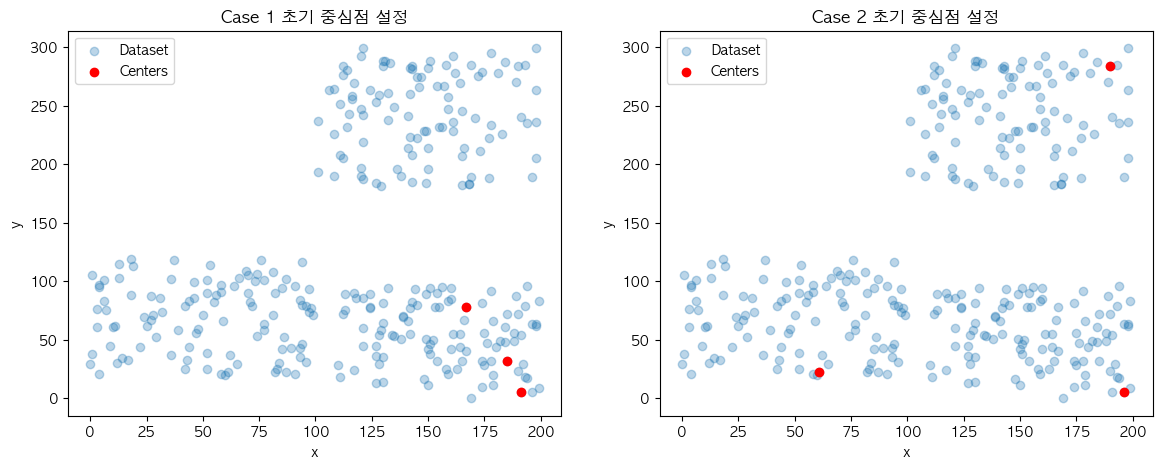
위와 같이 같은 데이터 집합 내에서 다른 초기 중심점 케이스로 시작하는 2개의 KMeans 모델이 있을 때 어느 모델이 더 빠르게 학습을 마무리할까요?
❌ Case 1
⭕️ Case 2
학습 시간 지연은 실행 때마다 달라지는 초기 중심점의 위치로부터 발생합니다. 2개의 모델이 만들어낸 최종 군집 결과물은 크게 다르지 않다는 것을 확인할 수 있는데요. 이와 같이 결과물을 미리 알고 초기 중심점을 다시 보았을 때 보다 학습을 빠르게 완료한 Case 2의 시작점이 Case 1 보다 최종 결과물을 만드는 데에 유리하다는 것을 알 수 있습니다.
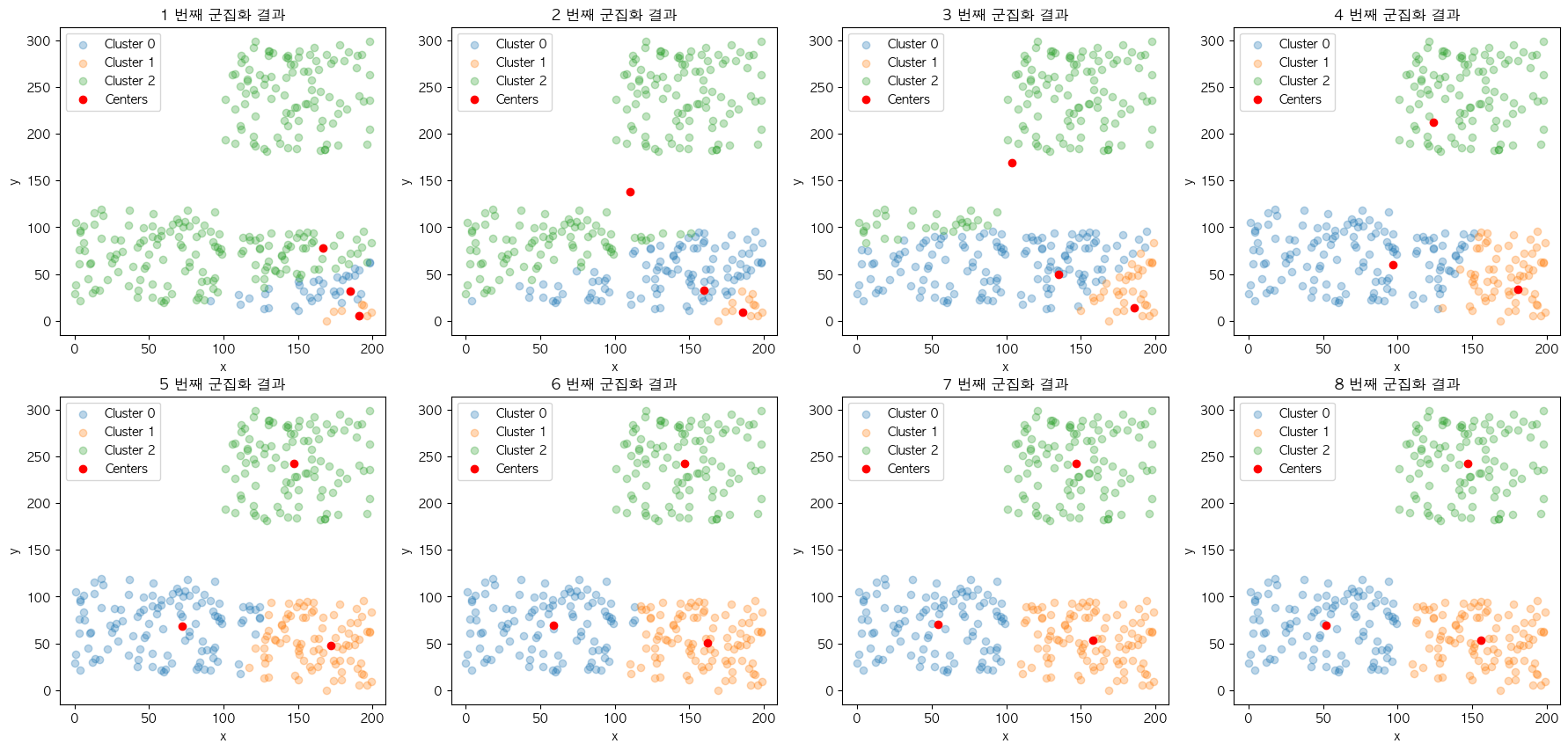
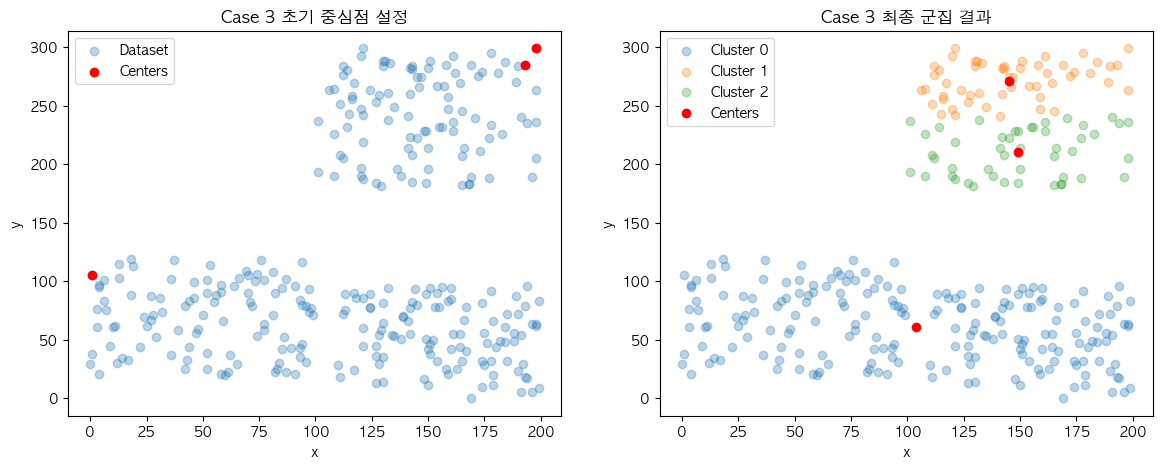
❓ Case 3
❓ Case 4
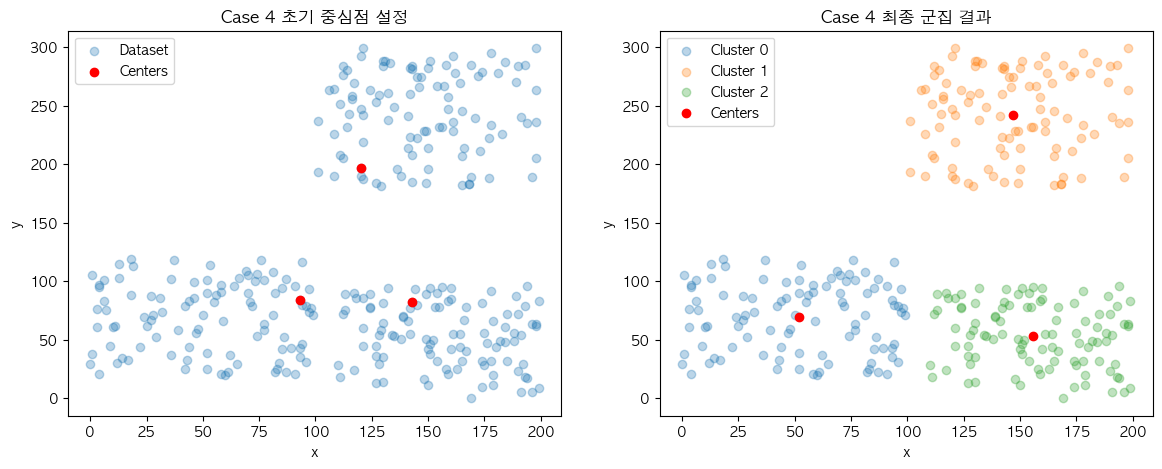
결과의 불규칙성도 같은 이유에서 나타납니다. 현재 설명에 사용 중인 데이터 집합은 결과의 차이가 명확하게 보일 정도의 군집 결과가 2개로 나누어지도록 의도하고 구성했는데요. 이에 따라 Case 3과 Case 4의 결과가 초기 중심점의 위치에 따라 최종 군집 결과가 다르게 나오는 것을 확인할 수 있습니다.
❗️ KMeans++ Process
- 첫 번째 중심점을 무작위로 설정
- 설정된 중심점과 데이터 간의 거리 계산
- 거리의 총합이 최대인 데이터 포인트를 다음 중심으로 설정
- 2~3의 과정을 설정된 K 변수 만큼의 중심점이 설정될 때 까지 반복
KMeans++는 이러한 성능과 결과의 불규칙성을 완화시키기 위한 초기 중심점 설정 프로세스를 제시해 줍니다. 우리는 학습 시간 지연의 상황에서 중심점들 간의 응집도가 낮았을 때 더욱 빠르게 마무리되는 것을 확인할 수 있었는데요. 이에 근거하여 K개의 초기 중심점들이 서로 거리가 멀도록 구성하는 것이 해당 프로세스의 컨셉입니다.
K = 3
center_idx = np.random.choice(range(len(dataset)), size=1)
cluster_centers = dataset[center_idx]첫 번째 중심점을 무작위로 설정하는 것으로 시작하겠습니다. KMeans 설명 때와 동일하게 K 변수는 3으로 설정되어 있습니다. 하지만 하나의 중심점만 무작위로 고르기 위하여 해당 메서드의 size 매개변수로 1을 전달합니다.
distances = euclidean_distances(dataset, cluster_centers)설정된 중심점과 데이터 간의 거리 계산은 데이터 집합과 점차 하나씩 추가될 중심점 집합을 대상으로 진행합니다.
total_distances = distances.sum(axis=1)
next_center_idx = total_distances.argmax()
cluster_centers = np.append(cluster_centers, dataset[[next_center_idx]], axis=0)거리의 총합이 최대인 데이터 포인트를 다음 중심으로 설정 단계에서 해당 거리 정보를 이용하는데요. 이 때의 행위는 확률적으로 현재 시점에 설정된 모든 중심점들과 가장 멀리 떨어진 데이터를 선택되도록 합니다.
# 4. 2~3의 과정을 설정된 K 변수 만큼의 중심점이 설정될 때 까지 반복
while len(cluster_centers) < K:
# 2. 설정된 중심점과 데이터 간의 거리 계산
distances = euclidean_distances(dataset, cluster_centers)
# 3. 거리의 총합이 최대인 데이터 포인트를 다음 중심으로 설정
total_distances = distances.sum(axis=1)
next_center_idx = total_distances.argmax()
cluster_centers = np.append(cluster_centers, dataset[[next_center_idx]], axis=0)2~3의 과정을 설정된 K 변수 만큼의 중심점이 설정될 때 까지 반복 시킵니다.
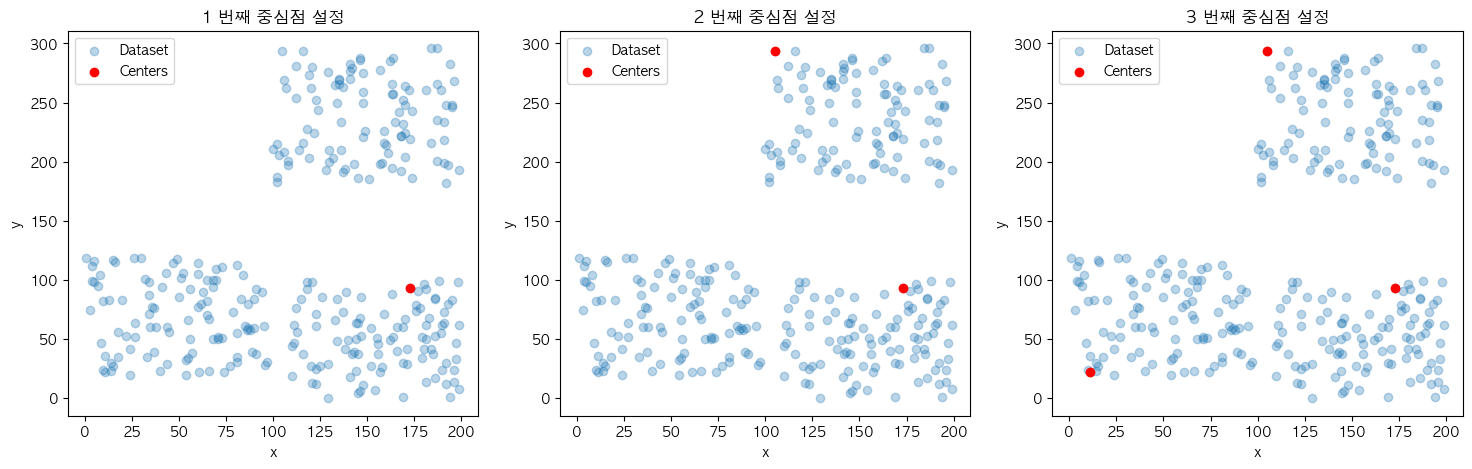
이제 작성된 KMeans++ 프로세스를 적용시켰을 때 설정되는 초기 중심점들의 시각화를 확인하면 서로 멀리 떨어진 데이터 포인트들이 설정된 것을 볼 수 있습니다.
💥 KMeans and KMeans++ Difference
그러면 이제 기존 KMeans와 비교했을 때의 의문점이 생기실 텐데요.
🌈 Comparison Test
- 초기 중심점 평균 거리
- 프로세스 반복 횟수 집계
- 결과의 군집 구조
저의 고민 범위 내에서는 무작위 방식과 비교했을 때 초기 중심점들이 서로 멀리 떨어지게 만들어지는지, 빠르게 학습을 마무리 하는지 그리고 결과가 일정하게 나타나는지로 3가지의 케이스가 일반적일거라고 생각을 하는데요.
kmeans_init_centers = list()
kmeans2_init_centers = list()
for i in range(100):
# kmeans
kmeans = KMeans(K=3)
kmeans_init_centers.append(kmeans.init_centers(dataset))
# kmeans++
kmeans2 = KMeans2(K=3)
kmeans2_init_centers.append(kmeans2.init_centers(dataset))| KMeans | KMeans++ | |
| 1 | [113, 214], [ 54, 107], [132, 192] (88.87) | [143, 96], [189, 292], [ 11, 24] (224.47) |
| 2 | [146, 93], [194, 5], [ 37, 79] (127.9) | [ 38, 85], [189, 292], [194, 4] (240.01) |
| ... | ||
| 100 | [153, 291], [ 11, 52], [165, 50] (224.44) | [ 1, 62], [189, 292], [194, 4] (262.21) |
| mean | 132.9 | 235.6 |
초기 중심점들의 평균 거리의 측정 자료를 KMeans와 KMeans++를 여러번 실행시켜 구성하여 살펴보면 KMeans++가 KMeans에 비해 초기 중심점들의 거리를 넓히는 방식으로 구성하기 때문에 평균 거리가 더 높게 나오는 것을 볼 수 있었습니다.
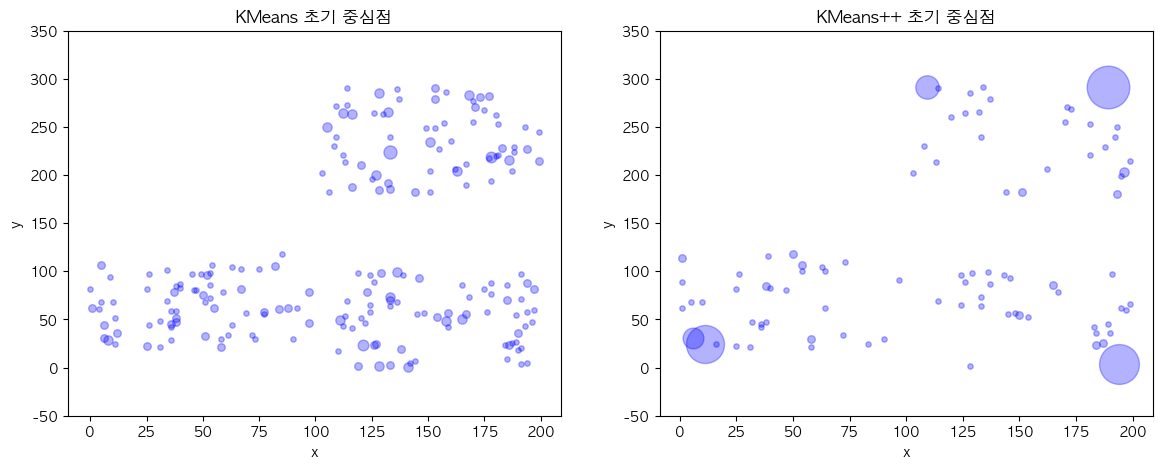
추가적으로 이와 같은 프로세스로 인하여 일관성 있게 포인트를 선택하는 것도 확인할 수 있었습니다.
kmeans_steps = list()
kmeans2_steps = list()
for i in range(100):
# kmeans
kmeans = KMeans(K=3)
kmeans_steps.append(kmeans.fit(dataset))
# kmeans++
kmeans2 = KMeans2(K=3)
kmeans2_steps.append(kmeans2.fit(dataset))| KMeans | KMeans++ | |
| count | 100 | 100 |
| mean | 4.82 | 3.55 |
| std | 1.578773 | 1.282162 |
| min | 2 | 2 |
| 25% | 4 | 2 |
| 50% | 5 | 4 |
| 75% | 6 | 5 |
| max | 11 | 7 |
프로세스 반복 횟수 집계의 확인은 불규칙한 성능 문제점과 관련이 있는 실험 입니다. KMeans++도 초기 중심점 중에서 기준이 되는 첫 번째 중심점을 선택함에 있어서는 무작위 방식을 사용하기 때문에 성능의 불규칙성은 존재하기 마련이지만 위의 측정 결과를 확인해보았을 때 많은 완화를 보여주고 있는 것을 확인할 수 있습니다.
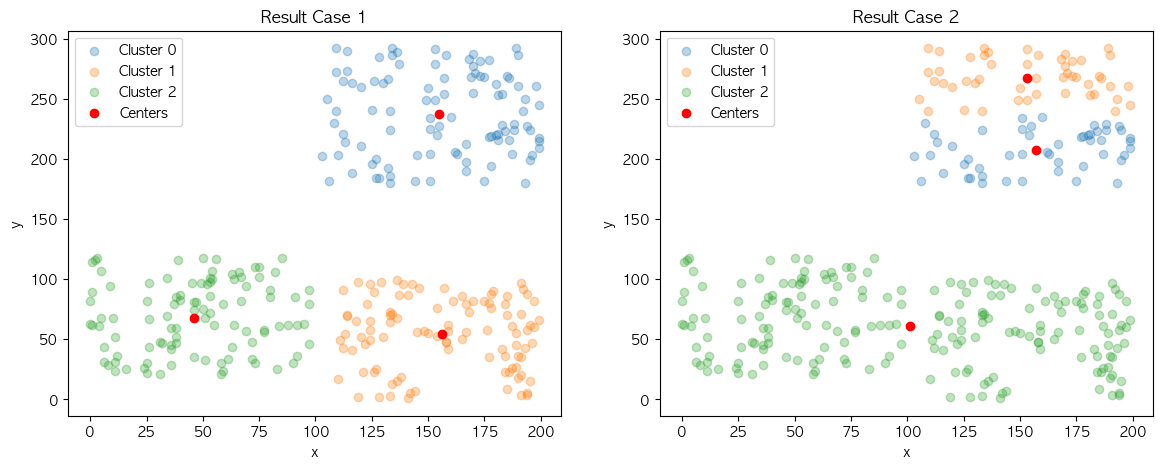
결과의 군집 구조는 결과의 불규칙성을 확인해보는 실험입니다. 제가 구성한 데이터 집합은 이전에 설명드렸듯이 K를 3으로 설정한 군집화를 수행할 경우 2가지의 구조로 나오는 것을 의도하여 제작했습니다.
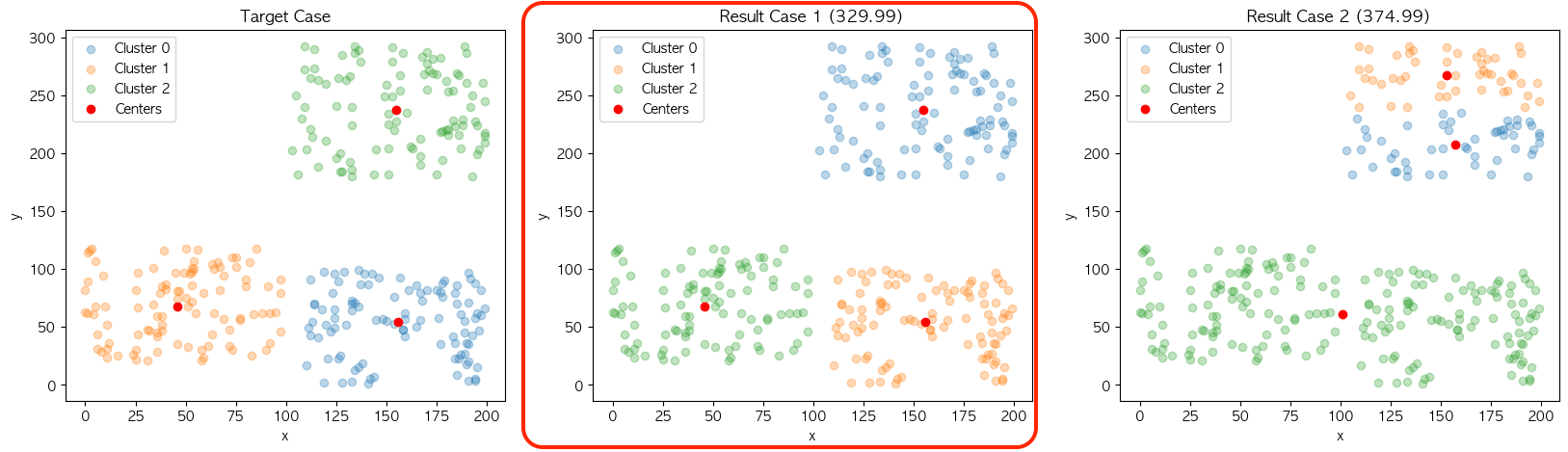
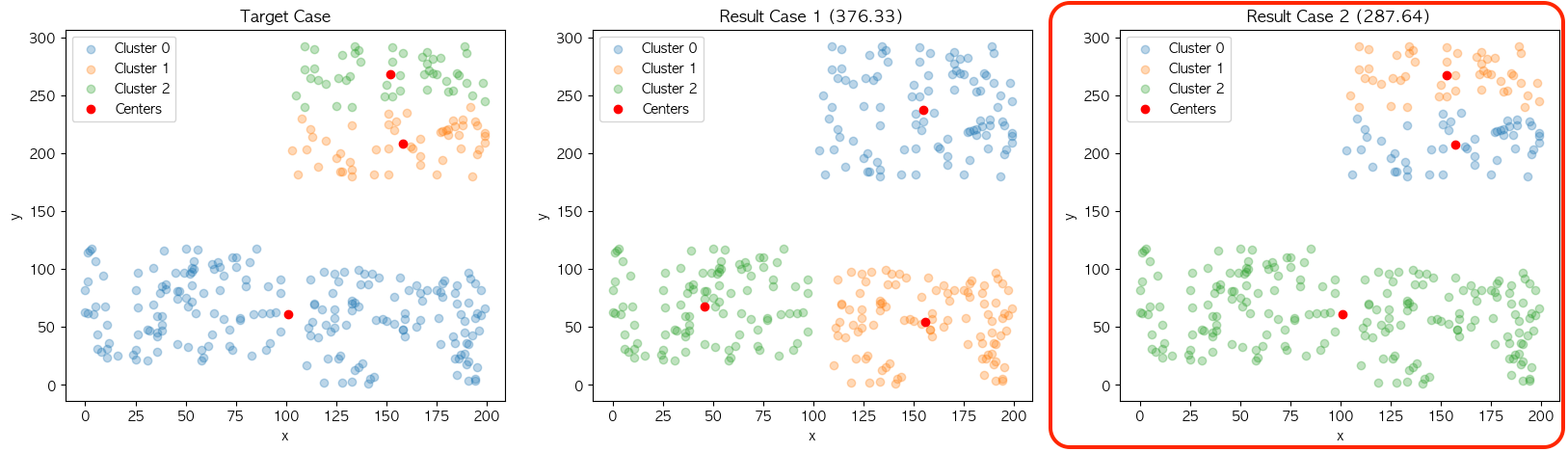
결과의 불규칙성을 실험하기 위한 과정은 다음과 같습니다. 위와 같이 KMeans의 최종결과에 설정된 중심점의 위치와 2가지 케이스 별 각 군집의 중심점값을 비교하여 총합을 계산하였을 때 최소 거리의 케이스를 해당 모델의 군집 구성으로 카운트 합니다.
| KMeans | KMeans++ | |
| case 1 | 82 | 99 |
| case 2 | 18 | 1 |
대부분의 결과가 case 1을 가지는 것을 볼 수 있는데요. 큰 차이는 없지만 KMeans가 KMeans++에 비해 빈번하게 case 2의 군집구성을 만드는 현상을 보여주면서 KMeans++의 결과의 불규칙성 완화도 확인할 수 있었습니다.
| KMeans | KMeans++ | |
| 1 | K개의 초기 중심점 설정 | 첫 번째 중심점을 무작위로 설정 |
| 설정된 중심점과 데이터 간의 거리 계산 | ||
| 거리의 총합이 최대인 데이터 포인트를 다음 중심으로 설정 | ||
| 설정된 K 변수 만큼의 중심점이 설정될 때 까지 반복 | ||
| 2 | 중심점과 데이터 간의 거리 계산 | |
| 3 | 최소 거리 중심점의 군집 번호를 데이터에 부여 | |
| 4 | 군집 별 평균값을 계산하여 중심점에 반영 | |
| 5 | 2~4의 과정을 중심점에 변화가 없을 때 까지 반복 | |
KMeans++는 기존 KMeans의 성능과 결과의 불규칙성을 완화하기 위한 하나의 제안으로, KMeans의 무작위 방식이 무조건 틀리지는 않습니다. 목적에 따라 불규칙성은 예기치 못한 좋은 결과를 가져다줄 수도 있으니까요. 혹은 제가 설명해 드린 것 외에도 다른 관점에서의 문제를 완화하기 위한 다른 알고리즘을 사용할 수도 있고요. 😎😎
스터디의 최종 목표인 Typescript로 구현해 보는 KMeans를 작업하기 위한 모든 지식이 탄탄하게 쌓아졌습니다. 이제 다음 챕터에서 전에 배운 Iteration Protocol도 살짝 얹어서 구현해 보면 되겠네요. 다음 주에 다시 찾아 뵙겠습니다. 오늘 하루도 수고 많으셨어요. ☺️☺️
'@dev.formegusto' 카테고리의 다른 글
| 섬세한 머신러닝과 딥러닝의 차이점 (2) Mechanism Perspective (0) | 2024.04.17 |
|---|---|
| 섬세한 머신러닝과 딥러닝의 차이점 (1) Chaos: Machine Learning? Deep Learning? (0) | 2024.02.21 |
| Typescript로 구현해 보는 KMeans (4) KMeans With UI Interaction (1) | 2024.02.07 |
| Typescript로 구현해 보는 KMeans (3) KMeans++ with Typescript (0) | 2024.01.17 |
| Typescript로 구현해 보는 KMeans (1) Javascript Iteration Protocol (1) | 2024.01.03 |
